Outreach & Media

I enjoy sharing the excitement and creativity of mathematics, through public talks, quirky side projects and media appearances. I’ve spoken to a wide range of audiences: from large KS4 and A-level enrichment days, to academic colloquia, the Royal Institution and to listeners on BBC Sounds.

This page collects some of my favourite outreach activities, fun mathematical investigations and media highlights. If you’re interested in booking a talk, featuring a project, or collaborating on something new, get in touch. For academic talks related to my research, see my research page.

Highlights

▶️ Matt Parker’s video on my optimal coin analysis – We can fix UK currency with a £1.75 coin
▶️ 5-min video: The quest to find every UK bridge height sign – from MathsJam
📗 Chalkdust issue 21 out now – our magazine for the mathematically curious
📰 Media coverage: The maths of chocolate fountains – the Washington Post, Smithsonian Magazine and more

The maths of chocolate fountains

My most popular 1-hour talk exploring real research into non-Newtonian fluids, falling chocolate, and ketchup fountains. With live demos and actual chocolate. Good for all ages.

📰 Newspaper coverage: Washington Post, Smithsonian Magazine, Mail Online.
▶️ Radio interviews: Heart Breakfast with Ed & Rachel, BNR (in Dutch)

Read more about the maths of chocolate fountains talk and research project.

Making coins better: A call for change

What makes a good set of coins? Using real shopping data and maths, we discover why the UK should consider a £1.23 coin. Or maybe a £1.75 coin. Or a £1.33 coin…

▶️ My episode of Radio 4’s Boring Talks on BBC Sounds
▶️ Matt Parker’s video on my analysis
📖 Forget a new £1 coin, we need a £1.23 coin
📖 Why self-service machines give such awful change

The quest for every bridge height sign

In the UK, bridge clearance signs display both imperial and metric measurements. This means there are way more combinations than you’d expect. Can I find them all?

▶️ Watch my 5-minute MathsJam talk
🔎 Explore the full bridge sign catalogue

Chalkdust magazine

Our magazine for the mathematically curious, which I co-founded in 2015. Prints 3000 copies twice a year and ships in bulk to 29 UK universities and individually worldwide. An entertaining mix of interesting mathematics, puzzles and daft jokes. Free to read online.

📗 Chalkdust magazine

VisualPDE: Real-time insight into mathematical models

Many real-world phenomena – from heat flow to bacterial growth to population spread – can be modelled using partial differential equations (PDEs). But solving and visualising these equations has traditionally required coding and technical expertise. VisualPDE changes that: it’s an interactive, browser-based tool for exploring PDEs in real time. Whether you’re teaching, researching or persuading stakeholders, VisualPDE makes your models clear, dynamic and compelling.

💻 VisualPDE.com

Is there a perfect maths font?

An illustrated, surprisingly funny tour through the history of maths typesetting, with a hunt for the best font.

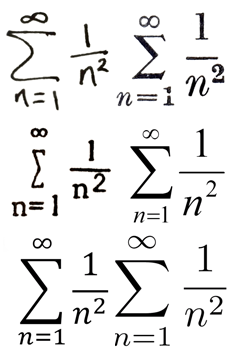
📖 Is there a perfect maths font?

Things I wish I knew about scientific computing before I started scientific computing

A reflective talk for science postgraduates on lessons learnt in a decade of scientific coding – from version control to debugging and thinking like a scientist. For the novice, I provide a broad sense of the landscape and guidance on where to start. For the expert, I provide tips on how to boost your productivity.

Other outreach articles

📖 Stopping distances in the Highway Code are wrong
📖 The maths of music
📖 Fun with water bells