Research
Broadly speaking, I am interested in developing mathematical, computational techniques to investigate complex, weirdly-behaving fluids.
These fluids are found everywhere in industry and nature, and their behaviour is often due to complex microscopic structure. This structure could come from a large number of suspended particles, a network of connected fibres, or the presence of swimming microorganisms.
My approach is to combine careful mathematical modelling of this microstructure with novel, efficient methodologies for high-performance computing. This allows me to run very large yet very detailed simulations of these fluids, helping us better understand the resultant macroscopic behaviour.
Recently, I have also become interested in using the latest web technology to solve scientific problems. Check out VisualPDE.com, a project I’m working on with Ben Walker and Andrew Krause, where you can solve nonlinear PDEs interactively in real time, in your browser or on your phone.
Details of the projects I have been involved with are described here.
Publication list
You can also view my outputs on Google Scholar.
Undulatory swimming in suspensions and networks of flexible filaments.
Journal of Fluid Mechanics 993, A10. [Read more]
Stokesian Dynamics in Python.
Journal of Open Source Software 9(94), 6011 [Read more]
Generating, from scratch, the near-field asymptotic forms of scalar resistance functions for two unequal rigid spheres in low Reynolds number flow.
Physics of Fluids 35(12), 127126 [Read more]
VisualPDE: rapid interactive simulations of partial differential equations.
Bulletin of Mathematical Biology 85, 113 [Read more]
Methods for suspensions of passive and active filaments.
Journal of Computational Physics 424, 109846 [Read more]
Shear-thickening fluids in biologically relevant agents.
Biorheology 56(1), 39–50. [Read more]
Small- and large-amplitude oscillatory rheometry with bead–spring dumbbells in Stokesian Dynamics to mimic viscoelasticity.
Journal of Non-Newtonian Fluid Mechanics 261, 136–152 [Read more]
Anomalous effect of turning off long-range mobility interactions in Stokesian Dynamics.
Physics of Fluids 30(7), 077103 [Read more]
Frictional shear thickening in suspensions: The effect of rigid asperities.
Physics of Fluids 29(12), 121607. [Read more]
Simulations of a heavy ball falling through a sheared suspension.
Journal of Engineering Mathematics 107(1), 179–200. [Read more]
The fluid dynamics of the chocolate fountain.
European Journal of Physics 37(1), 015803. [Read more]
Education papers
Going round in circles: Geometry in the early years.
Mathematics Teaching 286, 29–34. [Read more]
Developing ‘deep mathematical thinking’ in geometry with 3-and 4-year-olds: a collaborative study between early years teachers and university-based mathematicians.
Mathematical Thinking and Learning 26(3), 306–325. [Read more]
PhD thesis
PhD thesis: The mechanics of suspensions
This became the papers published in 2017 and 2018.
Projects
VisualPDE.com: Interactive solutions to PDEs in your browser
Many real life phenomena can be described as quantities changing in time or space: heat spreading, bacteria reproducing, populations invading. These can often be described using partial differential equations (PDEs), whose solutions can be tricky to find and gain intuition for since they are hard to draw on paper. Until now, numerical solutions had to be coded up in a programming language.
But not any more! Ben Walker, Andrew Krause and I have been working on VisualPDE.com, where you can solve nonlinear PDEs interactively in real time, in your browser or on your phone, with no programming knowledge required. In fact, the simulation you see here is live and interactive: give it a click!
We hope VisualPDE does to PDEs what Desmos did to graph plotting. Totally customisable, lightning fast and delightfully embeddable: let us know how you use it, in your research and your teaching!
- VisualPDE.com
- GitHub: Open source GitHub repo
VisualPDE: rapid interactive simulations of partial differential equations.
Bulletin of Mathematical Biology 85, 113
Locomotion of sperm swimming through mucus

Mucus is a complex fluid with lots of structure which is about the same size as the sperm. We are modelling sperm swimming through such a structured environment, looking at how different swimming patterns interact with different structures. Since experiments are currently unable to probe these interactions, these simulations hope to reveal the selection mechanism.
Undulatory swimming in suspensions and networks of flexible filaments.
Journal of Fluid Mechanics 993, A10.
Large-scale simulation of flexible filament suspensions

This has involved looking at the behaviour of thousands of flexible filaments sedimenting through a viscous fluid, discovering the consequences of flexibility. We’ve also looked at populations of swimming filaments as part of the sperm project detailed below. And we’ve looked at arrays of beating cilia, seeing how they coordinate (or not!) with each other.
- GitHub: Flexible filament simulation codes for both 2D and 3D in Matlab
Methods for suspensions of passive and active filaments.
Journal of Computational Physics 424, 109846
Shear thickening in suspensions
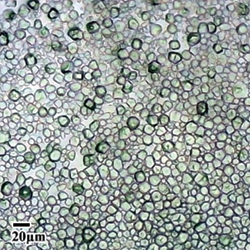
Image: Peter Kilbride
Current research suggests that the secret lies in contact forces between particles, yet these are usually implemented in an ad hoc way, resulting in inaccurate predictions or high computational cost. We developed a new method which allows us to investigate contact models quickly and efficiently, and suggests an important factor in models of strongly shear-thickening fluids.
Frictional shear thickening in suspensions: The effect of rigid asperities.
Physics of Fluids 29, 121607.
Shear-thickening fluids in biologically relevant agents.
Biorheology 56(1), 39–50.
Tracking a ball falling through a dense suspension

We investigated the structure of the small particles caused by an applied oscillatory shear and the heavy ball, and offered some explanations and a mechanism for this peculiar observation.
Simulations of a heavy ball falling through a sheared suspension.
Journal of Engineering Mathematics 107(1), 179–200.
Modelling non-Newtonian fluids as suspensions
Methods of simulating particles in viscous, Newtonian fluids are widely accepted, but when the background fluid is non-Newtonian, the standard methods begin to fail. Unfortunately, many common real-life suspensions—concretes, paints—behave like this. One solution is to ‘fake’ a non-Newtonian liquid by placing little springs in a Newtonian background fluid.
We simulate suspensions of bead-and-spring dumbbells with various force laws, placing them under standard rheological tests, to see how good a representation of real non-Newtonian fluids they are. We see how certain parameters in the models lead to the suspension exhibiting useful properties, as well as explain how to extract this information from simulations.
Small- and large-amplitude oscillatory rheometry with bead–spring dumbbells in Stokesian Dynamics to mimic viscoelasticity.
Journal of Non-Newtonian Fluid Mechanics 261, 136–152
Stokesian Dynamics
Many of my computer simulations are performed using a technique called Stokesian Dynamics. It’s a good technique for simulating systems of spherical particles in a low-Reynolds number regime where you know the forces acting on the particles, and you want to know where they go. In suspension, particles can act indirectly on each other as well as directly, moving the fluid around them as they move, which in turn moves other particles. This behaviour is captured nicely in this method.
Both long-range hydrodynamics and lubrication are included in Stokesian Dynamics, and the method is suited to three-dimensional simulation in both periodic and non-periodic domains, with relatively low calculation and time penalty. We give a complete and thorough explanation of Stokesian Dynamics and provide a walkthrough of how to write your own implementation of it.
I have written a complete implementation of Stokesian Dynamics, allowing particles of different sizes, in Python (with some speed enhancements). It is available on GitHub with an associated paper in the Journal of Open Source Software.
- GitHub: Stokesian Dynamics in Python
Stokesian Dynamics in Python.
Journal of Open Source Software 9(94), 6011
Generating, from scratch, the near-field asymptotic forms of scalar resistance functions for two unequal rigid spheres in low Reynolds number flow. [Corrections to Jeffrey & Onishi (1984)]
Physics of Fluids 35(12), 127126 [Read more]
PhD thesis: The mechanics of suspensions.
Chapter 2 contains the details on Stokesian Dynamics.
Chocolate fountains

- Read more about the fluid dynamics of chocolate fountains
The fluid dynamics of the chocolate fountain.
European Journal of Physics 37(1), 015803.
Conferences and seminars
Have we met recently? Perhaps it was at one of these events. If you’d like me to talk at your seminar series, get in touch.
Selected recent and international talks:
- Bristol Engineering Mathematics seminar series, December 2023
- Cambridge Biomaths lunchtime seminar series, November 2023
- Strathclyde applied maths seminar series, November 2023
- SIAM Conference on Computational Science and Engineering (CSE23): Amsterdam, February 2023
- International Congress on Rheology, Rio de Janeiro, December 2020
- Fluids & Elasticity, Malaga, June 2019
- Annual European Rheology Conference, Portorož, April 2019
- SIAM Conference on Computational Science and Engineering (CSE19): Spokane, February 2019